كيف تفهم شرح درس تمثيل الدوال التربيعية بيانيا بسهولة؟ شرح مفصل بالخطوات والأمثلة

إن شرح درس تمثيل الدوال التربيعية بيانيا يعد من أهم محاور مادة الرياضيات في المرحلة المتوسطة، إذ يُمكّنك من تحليل الرسوم البيانية وفهم العلاقة بين المتغيرات من خلال تمثيل بياني واضح يُظهر شكل الدالة وسلوكها. وفي هذا المقال، نقدم لك شرحاً مفصلاً ومبسطاً مع أمثلة تساعدك على الفهم والتطبيق بثقة.

شرح درس تمثيل الدوال التربيعية بيانيا

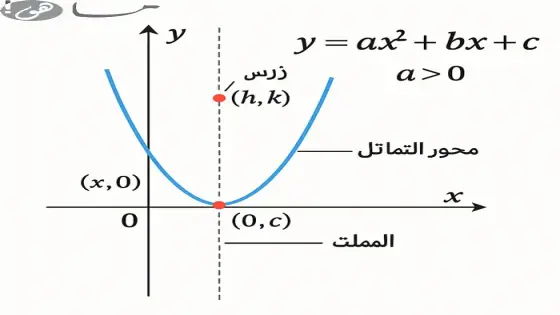
الدالة التربيعية هي دالة من الدرجة الثانية وتكتب على الصورة العامة:

y=ax2+bx+cy = ax^2 + bx + cy=ax2+bx+c

ويكون تمثيلها البياني قطعاً مكافئاً (Parabola).

• إذا كان $a>0$: المنحنى يتجه للأعلى.

• إذا كان $a<0$: المنحنى يتجه للأسفل.

خطوات تمثيل الدالة التربيعية على المستوى البياني

1. تحديد الشكل العام ومعاملات الدالة

ابدأ بتحليل الدالة وتحديد قيم $a$، $b$، و $c$.

2. حساب محور التماثل

معادلة محور التماثل هي:

x=−b2ax = -\frac{b}{2a}x=−2ab​

3. إيجاد إحداثيات الرأس

الرأس هو نقطة التماثل على الرسم البياني وتُحسب كما يلي:

x=−b2a,y=f(−b2a)x = -\frac{b}{2a}, \quad y = f\left(-\frac{b}{2a}\right)x=−2ab​,y=f(−2ab​)

4. تحديد نقطة التقاطع مع المحور الصادي

عند $x=0$، فإن $y=c$. وهي نقطة يسهل تحديدها مباشرة.

5. إيجاد الجذور إن وجدت

لحساب جذور المعادلة (التقاطع مع المحور السيني) استخدم القانون العام:

x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}x=2a−b±b2−4ac​​

6. إنشاء جدول القيم

اختَر قيمًا قريبة من قيمة $x$ في الرأس، واحسب $y$ المناظرة. استخدم التماثل لتقليل عدد الحسابات.

مثال تطبيقي على التمثيل البياني

الدالة:

y=x2−2x−3y = x^2 – 2x – 3y=x2−2x−3

• $a=1,b=-2,c=-3$

• محور التماثل: $x=1$

• الرأس: $(1,-4)$

• المقطع الصادي: $(0,-3)$

• الجذور: $x=3$ و$x=-1$

ارسم النقاط وقم بربطها بمنحنى سلس متماثل حول المحور.

أهم الخصائص التي يجب الانتباه لها

• المجال: جميع الأعداد الحقيقية

• المدى:

  • إذا كان $a>0$: من قيمة الرأس حتى ∞

  • إذا كان $a<0$: من -∞ حتى قيمة الرأس

• محور التماثل: خط رأسي يقسم المنحنى لنصفين متماثلين

• الرأس: أعلى أو أدنى نقطة في المنحنى

خلاصة الدرس وأهمية الفهم البصري

يساعد تمثيل الدوال التربيعية بيانياً على الربط بين الجبر والهندسة ويمنح المتعلم قدرة على تحليل المعادلات بصرياً. من خلال تتبع القواعد والخطوات المذكورة، تستطيع رسم أي دالة تربيعية بسهولة واستخلاص معلوماتها الدقيقة من التمثيل البياني.